Знайти площу сектора круга — не так складно, як здається на перший погляд. Достатньо знати два параметри: радіус круга та кут сектора (у градусах або радіанах). Навіть без калькулятора це можливо обчислити — якщо знати логіку, а не просто завчити формулу. У цій статті ми розберемо не лише саму формулу, але й типові помилки, лайфхаки для швидких обчислень і ситуації, коли ці знання реально допомагають у побуті.
Що таке сектор круга і чому ця фігура не така вже й «шкільна»
Сектор круга — це частина круга, обмежена двома радіусами та дугою. Найпростіше уявити собі шматок піци або частинку діаграми. Але це не просто абстракція зі шкільного підручника — подібні форми часто зустрічаються у повсякденному житті.
Наприклад, коли ви плануєте зробити клумбу у формі дуги, вирізаєте деталь з дерева чи будуєте альтанку, сектор стає дуже навіть реальним. Архітектори, інженери, дизайнери інтер’єрів — усі вони мають справу з подібними обчисленнями.
Основна формула площі сектора круга
Щоби обчислити площу сектора, потрібно знати центральний кут і радіус круга. Якщо кут задано в градусах, використовується така формула:
S = (π × R² × α) / 360
де:
S — площа сектора,
R — радіус круга,
α — кут сектора (у градусах),
π ≈ 3,14.
Ця формула дозволяє знайти частину площі повного круга, яка відповідає заданому куту.
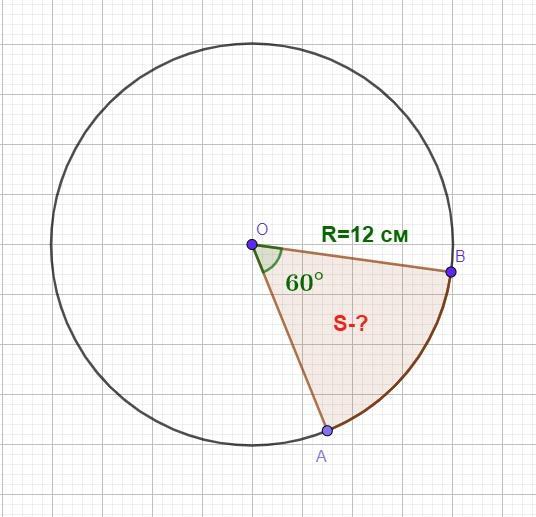
Приклад застосування формули
Припустимо, радіус круга дорівнює 12 см, а кут сектора — 90°. Тоді:
S = (3,14 × 12² × 90) / 360 = (3,14 × 144 × 90) / 360 = 1131,36 / 360 ≈ 3,14 × 36 = 113,04 см²
Порахувати — справа кількох хвилин. Але головне — зрозуміти, що відбувається: ми просто беремо частину від загальної площі круга.
Як діяти, якщо кут заданий у радіанах
У технічній або інженерній документації часто замість градусів використовуються радіани. У такому випадку формула інша:
S = 0.5 × R² × α
де α — кут у радіанах.
Щоб перевести градуси в радіани, просто скористайтеся перетворенням:
1 радіан ≈ 57,3°
Тож, якщо вам трапилася задача з кутом у радіанах — не панікуйте. Просто підставте значення у відповідну формулу.
Найпоширеніші помилки під час обчислень
Навіть знаючи формулу, можна легко схибити — особливо під час поспіху або невпевненості в одиницях виміру. Ось на що варто звернути увагу:
- Не переплутайте градуси з радіанами.
- Завжди перевіряйте, в яких одиницях подано радіус (сантиметри, метри).
- Уважно вводьте дані у калькулятор — помилка в одному символі може повністю змінити результат.
Корисні поради:
- Перед розв’язанням задачі обов’язково зробіть малюнок.
- Якщо потрібно знайти частину круга — подумайте, скільки всього таких частин утворюють повне коло.
- Використовуйте кругові діаграми для візуального розуміння секторів.
Альтернативна ситуація: що робити, якщо відомо лише довжину дуги
Буває, що у задачі замість кута дають довжину дуги (L). У такому випадку для обчислення площі сектора застосовується інша формула:
S = (L × R) / 2
Ця формула особливо корисна, коли ви маєте креслення або розгортку, де позначено тільки дугу.
Реальний приклад
Під час ремонту мені потрібно було виготовити дерев’яну накладку у формі дуги, що мала певну довжину. Не знаючи кута, я скористався саме цією формулою. Просто виміряв дугу рулеткою, визначив радіус — і за 2 хвилини отримав необхідну площу.
Чому варто знати ці обчислення — навіть якщо не працюєш з кресленнями
Можна подумати, що це знання потрібне лише школярам або будівельникам. Але ні — навіть у побуті ситуації, де знадобиться знайти площу сектора, не такі вже й рідкісні:
- Оформлення квітника чи ділянки.
- Побудова графіків і кругових діаграм.
- Виготовлення декору, вітражів, фанерних елементів.
- Підрахунок витрат тканини чи інших матеріалів у формі сектора.
Площа сектора — це не лише математика, а ще й творчість. Бо іноді від правильного розрахунку залежить, чи зійдеться візерунок, чи вистачить матеріалу, чи буде симетрія.
Ці знання — як універсальний інструмент у кишені: не використовуєш щодня, але в потрібний момент — безцінні.

Я копірайтерка, яка дихає словами й мислить заголовками. Перетворюю ідеї на тексти, що зачіпають, продають і запам’ятовуються. Якщо вашим словам не вистачає магії — я знаю, як її додати.