Бувають моменти, коли несподівано доводиться згадати шкільну геометрію — наприклад, під час ремонту, дизайну упаковки чи навіть творчих занять з дітьми. Здається, ну кому в реальному житті знадобиться шукати площу циліндра? А потім — хоп! — і ти стоїш із рулеткою біля газового балона або намагаєшся оцінити, скільки тканини піде на декоративну банку.
Щоб знайти площу циліндра, потрібно знати радіус його основи та висоту. Далі — підставляємо їх у формулу:
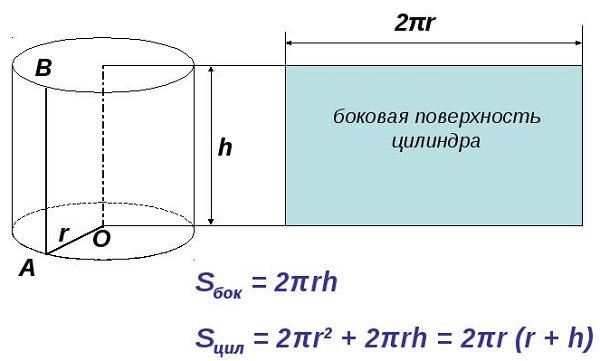
S = 2πr² + 2πrh,
де π ≈ 3.14, r — радіус основи, h — висота. Ця формула дає повну поверхневу площу, включаючи обидві круглі основи і бічну частину. Звучить трохи складно? Давайте розберемося крок за кроком.
Що таке циліндр і чому він не такий простий, як здається
Циліндр — це одна з базових об’ємних фігур, яка насправді трапляється в нашому житті набагато частіше, ніж ми помічаємо. Стакан, свічка, труба, банка, діжка, бочка — усе це його родичі. Він має:
- дві однакові круглі основи;
- бічну поверхню, яка за формою схожа на прямокутник, згорнутий у рулон.
І коли йдеться про площу, важливо не плутати, що саме ми хочемо знайти:
- тільки бічну поверхню (стінку);
- лише одну основу;
- або всю площу поверхні — тобто й основи, і стінку разом.
У кожному з цих випадків — своя формула. Але не хвилюйтесь, усе поясню — і без сухої теорії.
Формули, які справді варто знати
Щоб знайти площу циліндра, вам знадобляться лише радіус основи та висота. Усе решта — справа обчислень.
Площа бічної поверхні
Уявіть, що ви розгорнули циліндр — його стінка перетворилась би на прямокутник. Його висота — це висота циліндра, а довжина — довжина кола основи.
Формула:
S_бічна = 2πrh
Приклад:
Радіус = 5 см, висота = 12 см
S = 2 × 3.14 × 5 × 12 = 376.8 см²
Площа основи
Це просто площа круга. І так, у циліндрі дві основи — верхня і нижня.
Формула:
S_основа = πr²
Приклад:
Радіус = 5 см
S = 3.14 × 25 = 78.5 см²
Але якщо вам потрібно знайти повну площу, множимо на 2, бо основи дві.
Повна площа поверхні циліндра
Це вже вся фігура повністю — бічна поверхня плюс обидві основи.
Формула:
S_повна = 2πr² + 2πrh
Або спрощено:
S_повна = 2πr (r + h)
Приклад:
Радіус = 5 см, висота = 12 см
S = 2 × 3.14 × 5 (5 + 12) = 2 × 3.14 × 5 × 17 = 534.5 см²
Це і є загальна площа, яку, наприклад, треба обклеїти плівкою або пофарбувати.
У яких випадках площа циліндра має значення

Часто здається, що такі знання залишаються в стінах школи. Але насправді:
- Ви готуєте декор з банок і хочете точно знати, скільки піде матеріалу.
- Потрібно пофарбувати газовий балон або бочку — і важливо не купити зайвого.
- Рахуєте вартість друку на циліндричних упаковках або етикетках.
- Плануєте ділянку з бочками, трубами або ємностями — потрібно знати площу для утеплення.
- Робите навчальний проект із дитиною і хочете показати приклад з життя.
Одного разу ми з колегою рахували, скільки тканини потрібно для пошиття чохлів на труби в інтер’єрі кафе. Виглядало божевільно, але в підсумку дуже врятувало бюджет — все зійшлося до сантиметра.
Часті помилки, які легко уникнути
Навіть найпростіші формули можуть дати збій, якщо щось не врахувати. Ось що трапляється найчастіше:
- Переплутали радіус і діаметр. Радіус — це половина діаметра. Не забудьте поділити на 2, якщо заданий діаметр.
- Змішані одиниці. Не змішуйте сантиметри з метрами — це ламає все. Переведіть усе до однієї системи.
- Забули про другу основу. Якщо шукаєте повну площу, множимо площу круга на 2.
- Неправильно округлили. Особливо в задачах із точністю — зазначайте, з яким π працюєте: 3.14, 22/7 чи залишаєте π у вигляді символу.
- Не вказали одиниці. Без цього обчислення можуть бути безглуздими. Завжди додавайте см², м² тощо.
Невеличкий лайфхак — як усе це запам’ятати
Я завжди уявляю собі циліндр як торт у коробці:
- Дно — кругла основа,
- Кришка — друга основа,
- Стінка — бокова поверхня, обгорнута етикеткою.
І от щоб порахувати, скільки потрібно «обгортки», ми міряємо коло × висоту. А щоб покрити зверху і знизу — рахуємо площу круга × 2.
Це допомагає не лише дітям, а й дорослим. Бо іноді в голові формули зникають, а торт — ні.
Підсумовуючи, не бійтеся задач про площу циліндра. Варто раз розібратись — і формули починають працювати на вас. Усе стає логічним і навіть приємно зрозумілим. А якщо раптом виникне потреба згадати, просто погляньте на найближчий стакан — він і є ваша підказка.

Я копірайтерка, яка дихає словами й мислить заголовками. Перетворюю ідеї на тексти, що зачіпають, продають і запам’ятовуються. Якщо вашим словам не вистачає магії — я знаю, як її додати.